Stress Testing. Finding edge cases where our algorithm fails

We will see a powerful technique, called Stress Testing, to test the correctness of our programming solution. Often, in competitive programming, We come across scenarios where our solution gives us wrong answers, although the solution seems to be 100% correct. Sometimes, we are stuck in some edge cases. Well, a popular competitive programming platform like codechef does not reveal those test cases. How to find out that? Even after scratching your head for hours, you fail to find it out. You can try "Stress Testing". If you are not new to competitive programming you must know about it, but this can be a savior if you are a newbie.
What is stress testing?
To quote Wikipedia:
Stress testing (sometimes called torture testing) is a form of deliberately intense or thorough testing used to determine the stability of a given system, critical infrastructure, or entity. It involves testing beyond normal operational capacity, often to a breaking point, to observe the results.
In other words, we will feed our solution with lots of randomly generated test cases and check the answer with the answer given by an alternative solution. This process is repeated until we reach a breakpoint. That is, the answers do not match. The alternative solution must be absolutely correct.
For instance, I come up with a solution, let's say, A. And, I want to check its correctness. What I will do is think of an alternative naive but correct solution, let's say, B. Secondly, I will generate some random inputs and match answers of both the solution: A and B. We will repeat this process until we reach a breakpoint. That is, the answers do not match. Then our solution A is wrong because solution B always gives the correct answer. If we don't reach a breakpoint then our solution A is correct.
Why use it?
Without proving the correctness of your solution, you go all the way to code. Then after submitting your code, you get a Wrong answer splashed on your screen. That could be frustrating. Proving your solution before code comes under the best practices of competitive programming. This will save you a lot of hard work and time.
Let us understand Stress Testing with an example.
Problem: Find out the second-largest number from a given array.
Step 1: Think of a naive solution that must be correct.
Let us sort the array 'a' of 'n' numbers. After that, the number a[n-2] will be the second-largest number. Of course, we can do that in a much better way. We need not have to sort the entire array for this problem. I am just taking an example. Note that, this solution will always give the correct answer. We will call it find2MAXnaive.
C++ code:
int find2MAXNaive(int *a,int n){
sort(a,a+n);
return a[n-2];
}
Step 2: Think of a better solution.
We will first find out the largest number in O(n) time and then find the largest number X after excluding the largest number from the array. This X will be the second-largest number. We name this solution as find2MAXFast.
C++ code:
int find2MAXFast(int *a,int n){
int k, max1, max2;
max1 = max2 = INT_MIN;
for(int i = 0; i < n; i++){
if(max1 < a[i]){
max1 = a[i];
}
}
for(int i = 0; i < n; i++){
if(max2 < a[i] && a[i] != max1){
max2 = a[i];
}
}
return max2;
}
This solution appears to be correct. Right? Let us find it out using a stress test.
Step 3: Writing the stress testing code
C++ code:
int main()
{
int n,*a,i,c,ans1,ans2;
//stress test
c=1;
while(1){
//n will have any value from 2 to 10
n = rand()%9 + 2; // n = [2,10]
a = new int[n];
for(i = 0; i < n; i++){
//a[i] will have any value from 1 to 100
a[i] = rand()%100 + 1;// a[i] = [1,100]
}
// Now my random test data is ready.
//Checking if the answer from both the soultions match or not
if((ans1=find2MAXNaive(a,n)) == (ans2=find2MAXFast(a,n))){
cout<<"Test "<<c++<<": OK\n";
}
else {
cout<<"Error Found!\n";
cout<<"Result from naive solution: "<<ans1<<"\n";
cout<<"Result from fast solution: "<<ans2<<"\n";
cout<<"Test data:";
for(i = 0; i < n; i++){
cout<<" "<<a[i];
}
cout<<"\n";
break;
}
}
return 0;
}
What did I do in the above code?
- Inside the loop, first, I assigned a random value from 2 to 10 to n. Assigned a random value from 1 to 100 to each a[i].
- If the answers from both the solution match, we move on to the next iteration.
- If the answers from both the solution do not match, our solution find2MAXFast is not correct. We print the test data for which the answers do not match. And then, exited the loop.
Step 4: Let us run our code.
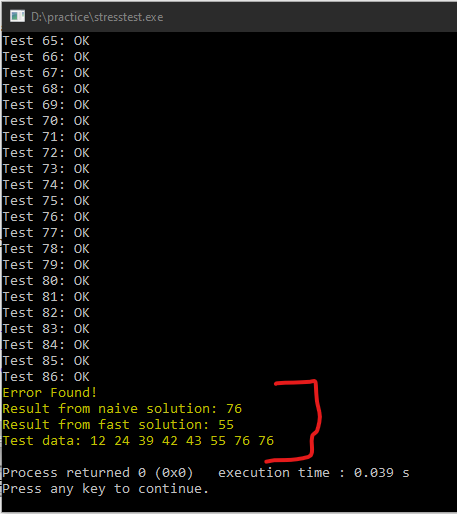
However, the test did not go as we expected. Our solution find2MAXFast gives the correct result for the first 86 cases. After that, it gives the wrong answer for the test case a = {12, 24, 39, 42, 43, 55, 76, 76} . The correct answer is 76 because we have two 76. So, it happens to be both the largest and the second-largest number.
Step 5: What was wrong with our solution?
Let us examine our code.
for(int i = 0; i < n; i++){
if(max2 < a[i] && a[i] != max1){
max2 = a[i];
}
}
We matched a[I] with max1. While doing so, we ignored all the indices for which a[i] has the value equal to max1. We completely ignored the fact the same value can repeat itself at some other index. Instead, we should have gone for matching indices to ignore the largest number. In other words, we will store the index, let us say k, of the largest number. After that, to find out the second largest number, we will find the largest number for which index i is not equal to k.
Step 6: Correct our code.
C++ correct code for find2MAXFast:
int find2MAXFast(int *a,int n){
int k, max1, max2;
max1 = max2 = INT_MIN;
for(int i = 0; i < n; i++){
if(max1 < a[i]){
max1 = a[i];
k = i;
}
}
for(int i = 0; i < n; i++){
if(max2 < a[i] && k != i){
max2 = a[i];
}
}
return max2;
}
Let's run our corrected code

By the time I took the screenshot, 1274397 test data were tested and none of them showed any error. You should wait for some time (let's say about 10 secs). If your loop continues to run without breaking, then congrats your solution is correct.
To view the source code on GitHub click here
Some points to know before considering stress testing.
- Your test data should be small for the naive solution to give results in less time. Yet, it should be diverse enough for covering almost all the test cases. Hence, generate your test data appropriately.
- This is not the full proof method to test the correctness of all the algorithms. There are situations for which the stress test method fails.
In conclusion, Stress Testing is a good tool but comes with its own drawbacks.